ЕГЭ-2021. Элементы математического анализа в составе профильного уровня
Новые формы обучения, инновации в обучении, введение современных технологий диктуют педагогу необходимость совершенствовать мастерство, а значит, и менять методы обучения и воспитания обучающихся.В по...
Новые формы обучения, инновации в обучении, введение современных технологий диктуют педагогу необходимость совершенствовать мастерство, а значит, и менять методы обучения и воспитания обучающихся.
В последние годы в содержание школьного курса все чаще закладывается алгоритмическая линия и применение алгоритмов является приоритетным.
Остановимся на задании 7 профильного уровня и на его примере разберем применение алгоритмов при решении задач.
Задание профильного уровня ЕГЭ относится к математическому анализу.
В этой задаче предлагается исследовать функцию с помощью:
При подготовке к ЕГЭ по математике задания 7 ЕГЭ профильного уровня вызывают значительную сложность у выпускников. Это, прежде всего, продиктовано неумением учащихся внимательно «вчитываться» в текст задания, тем, что ребята путают обозначения при заданиях на производную и первообразную, отвечают не строго на поставленный в задании вопрос.
Чтобы решить задания 7 ЕГЭ, нужно хорошо знать теорию производной, первообразной функции, уметь работать с текстом задания в КИМе ЕГЭ, ответить строго на поставленный в задании вопрос.
Так как задания 7 ЕГЭ очень разнообразны, то для облегчения работы можно составить алгоритмические задания 7 ЕГЭ для всех типов данного задания, которые позволяют учащимся структурировать теоретический материал и верно выполнить задание.
Возможные варианты применения алгоритмических карточек при подготовке к ЕГЭ:
– использовать карточки учителем в отдельности при объяснении решений данных заданий;
– использовать карточки учителем в комплексе на едином листе на уроках обобщающего повторения или на консультациях по подготовке к ЕГЭ;
– применять учащимися для самостоятельного, более осознанного решения заданий данного типа;
– для развития компьютерной грамотности при самостоятельном составлении алгоритмической карточки в электронном варианте;
– для дистанционного обучения учащихся.
Алгоритмические карточки по типам заданий
Алгоритмическая карточка по графику производной
Пример 1.
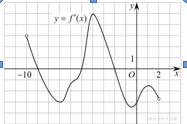
На рисунке изображен график производной функции f(x), определенной на интервале (-10;2). Найдите количество точек, в которых
f'(x)–2 касательная к графику функции f(x) параллельна прямой y=-2x−11 или совпадает с ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y=-2x−11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой y=–2. На данном интервале таких точек 5.
Ответ: 5.
Пример 2.
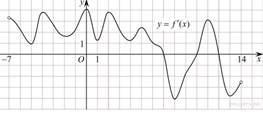
На рисунке изображен график производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x) на отрезке [-6; 9].
Решение:
Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [-6; 9] функция имеет одну точку максимума x=7.
Ответ: 1.
Алгоритмическая карточка по графику функции
Пример 1.
На рисунке изображен график функции y = f(x), определенной на интервале (-5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней.
Решение:
Поскольку касательная параллельна прямой y=6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. У данной функции производная равна нулю только в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y=6 или совпадает с ней в 4 точках.
Ответ: 4.
Пример 2.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение
Значение производной в точке касания равно угловому коэффициенту касательной, который, в свою очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A(1;2), B(1;-4), C(-2;-4). Угол наклона касательной к оси абсцисс будет равен углу ACB.
Ответ: 2.
Алгоритмическая карточка по графику первообразной
Пример 1.
На рисунке изображён график функции y=F(x) – одной из первообразных функции f(x), определённой на интервале (-3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [-2; 4].
Решение
По определению первообразной на интервале (-3; 5) справедливо равенство f(x)=F'(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x).
На рисунке точки, в которых выделены красным и синим цветом. Из них на отрезке [-2;4] лежат 10 точек (синие точки). Таким образом, на отрезке [-2;4] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Алгоритмическая карточка по графику производной от первообразной
Пример 1.
На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком, вычислите определенный интеграл ∫15f(x)dx.
Решение.
Определенный интеграл от функции y=f(x) по отрезку [1;5] дает значение площади подграфика функции f(x) на отрезке. Область под графиком разбивается на прямоугольный треугольник, площадь которого Sтр.= ∙2∙4=4, и прямоугольник, площадь которого Sпр=2∙4=8. Сумма этих площадей дает искомый интеграл
∫15f(x)dx=Sпр+Sтр.=8+4=12.
Ответ: 12.
Делая выводы, можно сказать, что теперь это самая сложная задача из негеометрических задач первой части экзамена. Средний процент правильных ответов к задаче 7 – 50,7%. Причины могут быть следующие:
В последние годы в содержание школьного курса все чаще закладывается алгоритмическая линия и применение алгоритмов является приоритетным.
Остановимся на задании 7 профильного уровня и на его примере разберем применение алгоритмов при решении задач.
Задание профильного уровня ЕГЭ относится к математическому анализу.
В этой задаче предлагается исследовать функцию с помощью:
- Графика самой функции. Обычно просят найти точку экстремума или интервал возрастания/убывания.
- Графика ее производной. В этом случае могут спрашивать что угодно: от всех тех же точек экстремума до касательных с заданным углом наклона. В зависимости от представленного графика принципиально различаются и методы решения задачи.
При подготовке к ЕГЭ по математике задания 7 ЕГЭ профильного уровня вызывают значительную сложность у выпускников. Это, прежде всего, продиктовано неумением учащихся внимательно «вчитываться» в текст задания, тем, что ребята путают обозначения при заданиях на производную и первообразную, отвечают не строго на поставленный в задании вопрос.
Чтобы решить задания 7 ЕГЭ, нужно хорошо знать теорию производной, первообразной функции, уметь работать с текстом задания в КИМе ЕГЭ, ответить строго на поставленный в задании вопрос.
Так как задания 7 ЕГЭ очень разнообразны, то для облегчения работы можно составить алгоритмические задания 7 ЕГЭ для всех типов данного задания, которые позволяют учащимся структурировать теоретический материал и верно выполнить задание.
Возможные варианты применения алгоритмических карточек при подготовке к ЕГЭ:
– использовать карточки учителем в отдельности при объяснении решений данных заданий;
– использовать карточки учителем в комплексе на едином листе на уроках обобщающего повторения или на консультациях по подготовке к ЕГЭ;
– применять учащимися для самостоятельного, более осознанного решения заданий данного типа;
– для развития компьютерной грамотности при самостоятельном составлении алгоритмической карточки в электронном варианте;
– для дистанционного обучения учащихся.
Алгоритмические карточки по типам заданий
Алгоритмическая карточка по графику производной
| В задании изображен график производной f'(x) | |||||||||
| Повторим: функция f(x), производная – f'(x), f'(x)=tg=k | Матери-альная точка | ||||||||
| В задании нужно найти: | V(t)=x'(t) a(t)= x''(t), где x(t) – закон движения, V(t) – скорость, a(t) – ускорение | ||||||||
| наим. f(x) на [a;b] | наиб. f(x) на [a;b] | точки экстремума | Убы-вает f(x) | Воз-раста-ет f(x) | касательная к f(x) параллельна прямой y=kx+b или совпадает с ней | ||||
| Решением является: | |||||||||
| на [a;b] гра-фик выше оси х | на [a;b] гра-фик ниже оси х | на [a;b] гра-фик выше оси х | на [a;b] гра-фик ниже оси х | (на оси x) | f'(x)<0 | f'(x)>0 | Проводим прямую у=к, и точки пересечения искомое | ||
| в а наим. значение | в b наим. значение | в b наиб. значение | в а наиб. значение | мах | min | Гра-фик ниже оси х | Гра-фик выше оси х | ||
| Гра-фик сверху вниз | Гра-фик снизу вверх | ||||||||
Пример 1.
На рисунке изображен график производной функции f(x), определенной на интервале (-10;2). Найдите количество точек, в которых
f'(x)–2 касательная к графику функции f(x) параллельна прямой y=-2x−11 или совпадает с ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой y=-2x−11 или совпадает с ней, их угловые коэффициенты равны –2. Найдем количество точек, в которых это соответствует количеству точек пересечения графика производной с прямой y=–2. На данном интервале таких точек 5.
Ответ: 5.
Пример 2.
На рисунке изображен график производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x) на отрезке [-6; 9].
Решение:
Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [-6; 9] функция имеет одну точку максимума x=7.
Ответ: 1.
Алгоритмическая карточка по графику функции
| В задании изображен график функции f(x) | ||||||||
| Повторим: функция – f(x), производная – f'(x), f'(x)=tg=k | ||||||||
| В задании нужно найти: | ||||||||
| с касательной, f'(x)=? (если касательной нет, то провести через указанные в условии точки) | f'(x)>0 | f'(x)<0 | f'(x)=0, кас. парал. прям. y=a | f'(x) не существ. | наим. f'(x) в точ-ках | наиб. f'(x) в точках | ||
| Решением является: | ||||||||
| (2 и 4 четв., окно) к=f'(x)=tg= | (1и3 четв., дверь) к=f'(x)=tg= | f(x) возрастает, поднимается | f(x) убывает, опускается | в точках max, min (верш., впадинах) | в острых пиках | наим. в той точке в кото-рой к=tg наи-меньшее | наиб. в той точке в которой к=tg наи-боль-шее | |
Пример 1.
На рисунке изображен график функции y = f(x), определенной на интервале (-5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=6 или совпадает с ней.
Решение:
Поскольку касательная параллельна прямой y=6 или совпадает с ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен значению производной в точке касания. У данной функции производная равна нулю только в точках экстремума функции. На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Таким образом, касательная к графику функции параллельна прямой y=6 или совпадает с ней в 4 точках.
Ответ: 4.
Пример 2.
На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение
Значение производной в точке касания равно угловому коэффициенту касательной, который, в свою очередь, равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A(1;2), B(1;-4), C(-2;-4). Угол наклона касательной к оси абсцисс будет равен углу ACB.
Ответ: 2.
Алгоритмическая карточка по графику первообразной
| В задании изображен график функции F(x) | ||||||||
| Повторим: функция (первообразная)- F(x), производная - f(x) F(x)== F(b)-F(a)=Sкрив.трапеции (a – начальная точка отрезка, b – конечная точка отрезка) | ||||||||
| В задании нужно найти: | ||||||||
| с касательной, f(x)=? (если касательной нет, то провести через указанные в условии точки) | f(x)>0 | f(x)<0 | f(x)=0, кас. парал. прям. y=люб. числу | f (x) не сущ. | наим. f(x) в точках | наиб. f(x) в точках | ||
| Решением является: | ||||||||
| (график во 2 и 4 четв., окно) к=f(x)=tg= | (график в 1 и 3 четв., дверь) к=f(x)=tg= | F(x) возрастает, поднимается | F(x) убывает, опускается | в точках max, min (верш., впадинах) | в острых пиках | наим. в той точке, в которой к=tg наименьшее | наиб. в той точке, в которой к=tg наибольшее | |
Пример 1.
На рисунке изображён график функции y=F(x) – одной из первообразных функции f(x), определённой на интервале (-3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [-2; 4].
Решение
По определению первообразной на интервале (-3; 5) справедливо равенство f(x)=F'(x)
Следовательно, решениями уравнения f(x)=0 являются точки экстремумов изображенной на рисунке функции F(x).
На рисунке точки, в которых выделены красным и синим цветом. Из них на отрезке [-2;4] лежат 10 точек (синие точки). Таким образом, на отрезке [-2;4] уравнение f(x)=0 имеет 10 решений.
Ответ: 10.
Алгоритмическая карточка по графику производной от первообразной
| В задании изображен график производной f(x) | |||||||||
| Повторим: функция (первообразная) – F(x), производная – f(x) F(x)== F(b)–F(a)=Sкрив.трапеции (a – начальная точка отрезка, b – конечная точка отрезка) | |||||||||
| В задании нужно найти: | Ин-те-грал=плошади кри-воли-ней-ной тра-пе-ции=раз-нос-ти пер-вооб-раз-ных | ||||||||
| Наим. F(x) на [a;b] | Наиб. F(x) на [a;b] | Точки экстре-мума | Бы-вает F(x) | Возрас- тает F(x) | Кас. к F(x) парал. прям. y=kx+b или совпада-ет с ней | ||||
| Решением является: | |||||||||
| На [a; b] гра-фик выше оси х | На [a; b] гра-фик ниже оси х | На [a; b] гра-фик выше оси х | на [a; b] гра-фик ниже оси х | (На оси x) | f(x)<0 | f(x)>0 | Прово-дим прямую у=к, и точки пересе-чения искомое | ||
| в а наим. Зна-чение | в b наим. Зна-чение | в b наиб. Зна-чение | в а наиб. Зна-чение | мах | min | график ниже оси х | Гра-фик выше оси х | ||
| график сверху вниз | график снизу вверх | ||||||||
Пример 1.
На рисунке изображен график некоторой функции y=f(x). Пользуясь рисунком, вычислите определенный интеграл ∫15f(x)dx.
Решение.
Определенный интеграл от функции y=f(x) по отрезку [1;5] дает значение площади подграфика функции f(x) на отрезке. Область под графиком разбивается на прямоугольный треугольник, площадь которого Sтр.= ∙2∙4=4, и прямоугольник, площадь которого Sпр=2∙4=8. Сумма этих площадей дает искомый интеграл
∫15f(x)dx=Sпр+Sтр.=8+4=12.
Ответ: 12.
Делая выводы, можно сказать, что теперь это самая сложная задача из негеометрических задач первой части экзамена. Средний процент правильных ответов к задаче 7 – 50,7%. Причины могут быть следующие:
- во-первых, эта задача на материал курса алгебры и начал анализа X – XI классов, для освоения которого необходима достаточная база знаний программы основной школы, которой, к большому сожалению, нет сейчас у многих старшеклассников;
- во-вторых, несмотря на невысокий уровень сложности самого задания, спектр проверки понимания темы «производная» в этом задании, к примеру, довольно широк: предлагаются и задачи на геометрический и механический смысл производной, и задачи с множеством ситуаций, описывающих связь между поведением функции и ее производной;
- в-третьих, для решения большинства задач 7 требуется не просто непосредственно применить алгоритм, что можно сделать, например, при решении простейших уравнений, а самостоятельно проанализировать ситуацию и сделать вывод. Даже в случае крайней простоты анализа все это требует от старшеклассников некоторых усилий, к которым не все готовы.
Гульназ КАШАПОВА,
учитель математики I квалификационной категории лицея-инженерного центра Советского района, г. Казань
Кадрия ШАКИРОВА,
доцент кафедры теории и технологий преподавания математики и информатики Института математики и механики им. Н.И.Лобачевского КФУ, кандидат педагогических наук
Язмага реакция белдерегез
Вход на сайт
РЕКОМЕНДУЕМ
Комментарийлар