ЕГЭ: Математика
Доценты кафедры теории и технологий преподавания математики и информатики Института математики и механики им. Н.И.Лобачевского КФУ Кадрия ШАКИРОВА, Наиля ТИМЕРБАЕВА и Эльмира ФАЗЛЕЕВА специально для...
Доценты кафедры теории и технологий преподавания математики и информатики Института математики и механики им. Н.И.Лобачевского КФУ Кадрия ШАКИРОВА, Наиля ТИМЕРБАЕВА и Эльмира ФАЗЛЕЕВА специально для читателей журнала «Магариф» подготовили статью, которая поможет подготовиться к ЕГЭ по математике.
Задачи по стереометрии высокого уровня сложности в ЕГЭ по математике профильного уровня предполагают построение и вычисление площадей сечений, а также расстояний и углов в пространстве.
Итоги экзаменов предыдущих лет показывают, что задачи по стереометрии по-прежнему являются самыми сложными и к их решению приступают не более трети выпускников, еще меньше выполняют их на максимальные два первичных балла.
Задания по стереометрии состоят из теоретической и вычислительной части. Причем 1 балл можно получить, если выполнен только один из пунктов: а) или б).
Чтобы успешно решать такие задачи, необходимо начать специальную подготовку уже в X классе. Прежде всего следует обратить внимание на знание теорем, формул, свойств геометрических фигур и тел. А также на так называемые «дежурные
факты», помогающие быстро вычислить некоторые величины (например, длины диагоналей квадрата или куба) или применить свойство, однажды доказанное (например, перпендикулярность скрещивающихся ребер правильного тетраэдра).
Особую сложность представляют задачи на нахождение расстояния между скрещивающимися прямыми. Учащимся необходимо не только знать методы решения данного типа задач, но и уметь применять их в зависимости от конкретного случая. В данной статье предлагаем различные методы нахождения расстояния между скрещивающимися прямы- ми – поэтапно-вычислительный, векторный, опорных задач и др., а также методика их применения.
Известно, что расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра. Но при решении задачи не всегда удается построить общий перпендикуляр. Поэтому нужно знать и уметь применять и другие методы.
Для нахождения расстояния между скрещивающимися прямыми можно использовать один из приведенных способов [1].
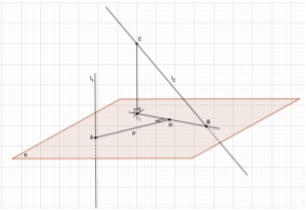
1. Метод построения общего перпендикуляра или поэтапно-вычислительный метод. В этом случае строится общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный каждой из них) и находится его длина.
2. Метод параллельных прямой и плоскости. В этом случае плоскость содержит одну из прямых и параллельна второй. Тогда искомое расстояние будет равно расстоянию от какой-нибудь точки второй прямой до построенной плоскости.
3. Метод параллельных плоскостей. В этом случае данные скрещивающиеся прямые заключаются в параллельные плоскости, проходящие через них, и находится расстояние между этими плоскостями.
Продолжение в документе
Задачи по стереометрии высокого уровня сложности в ЕГЭ по математике профильного уровня предполагают построение и вычисление площадей сечений, а также расстояний и углов в пространстве.
Итоги экзаменов предыдущих лет показывают, что задачи по стереометрии по-прежнему являются самыми сложными и к их решению приступают не более трети выпускников, еще меньше выполняют их на максимальные два первичных балла.
Задания по стереометрии состоят из теоретической и вычислительной части. Причем 1 балл можно получить, если выполнен только один из пунктов: а) или б).
Чтобы успешно решать такие задачи, необходимо начать специальную подготовку уже в X классе. Прежде всего следует обратить внимание на знание теорем, формул, свойств геометрических фигур и тел. А также на так называемые «дежурные
факты», помогающие быстро вычислить некоторые величины (например, длины диагоналей квадрата или куба) или применить свойство, однажды доказанное (например, перпендикулярность скрещивающихся ребер правильного тетраэдра).
Особую сложность представляют задачи на нахождение расстояния между скрещивающимися прямыми. Учащимся необходимо не только знать методы решения данного типа задач, но и уметь применять их в зависимости от конкретного случая. В данной статье предлагаем различные методы нахождения расстояния между скрещивающимися прямы- ми – поэтапно-вычислительный, векторный, опорных задач и др., а также методика их применения.
Известно, что расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего перпендикуляра. Но при решении задачи не всегда удается построить общий перпендикуляр. Поэтому нужно знать и уметь применять и другие методы.
Для нахождения расстояния между скрещивающимися прямыми можно использовать один из приведенных способов [1].
1. Метод построения общего перпендикуляра или поэтапно-вычислительный метод. В этом случае строится общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный каждой из них) и находится его длина.
2. Метод параллельных прямой и плоскости. В этом случае плоскость содержит одну из прямых и параллельна второй. Тогда искомое расстояние будет равно расстоянию от какой-нибудь точки второй прямой до построенной плоскости.
3. Метод параллельных плоскостей. В этом случае данные скрещивающиеся прямые заключаются в параллельные плоскости, проходящие через них, и находится расстояние между этими плоскостями.
Продолжение в документе












Комментарийлар