Алгоритмы в обучении математике
В настоящее время одной из центральных идей модернизации системы образования является компетентностный подход. Особенностью компетентностного обучения состоит не в усвоении готового знания, а в том, к...
В настоящее время одной из центральных идей модернизации системы образования является компетентностный подход. Особенностью компетентностного обучения состоит не в усвоении готового знания, а в том, как прослеживаются условия происхождения данного знания. Учащийся сам формулирует понятия, необходимые для решения учебной задачи, усваивает материал, являясь активным субъектом своего обучения. Учебная деятельность приобретает исследовательский и практико-ориентированный характер. При этом происходит развитие самопознания и самообразования личности.
Использование проблемного обучения на уроках математики помогает вызвать определенную познавательную потребность у учащихся и создать внутренние условия для успешного последующего усвоения материала. Технология проблемного обучения позволяет с помощью проблемных вопросов и учебных задач включить учащихся в исследовательскую деятельность, в том числе с целью открытия и построения алгоритмов, структурно-логических схем для решения предметных задач.
Приведем фрагмент урока математики в VI классе по теме «Масштаб» с использованием учебной задачи, направленной на самостоятельное открытие учениками алгоритма нахождения расстояния между двумя точками.
Вначале учащимся предлагается решить предметную задачу: «Определите время в пути автобуса, следующего из г. Казани в г. Елабугу, если скорость автобуса равна 60 км/ч.». При решении задания учащиеся сталкиваются с необходимостью узнать расстояние от одного города до другого, что определяется с помощью карты Татарстана. (Рис. 1)
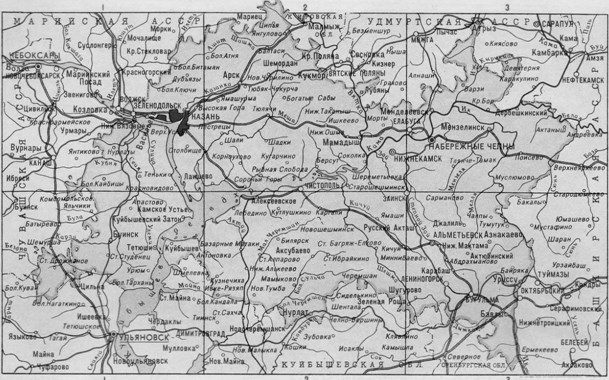
Рис. 1. Карта Татарстана.
В ходе беседы формулируется проблемный вопрос: как определить отношение длины отрезка на карте к длине соответствующего отрезка на местности?
В рассмотренном нами примере масштаб карты равен 1:30000000. Измерим длину отрезка на карте между двумя городами. Длина отрезка равна 6,1 см.
Обозначим длину отрезка на местности (в сантиметрах) буквой x и найдем отношение длины отрезка на карте к длине отрезка на местности: 6,1 : x, которое и будет равно масштабу карты. Значит, 6,1 : x = 1 : 30000000.
Решив полученное уравнение, имеем: x = = 183000000 (см) = 183000 (м) = 183 (км).
Возвращаясь к исходной задаче, определяем время в пути автобуса: t = ; t = = = 3,05 (ч).
Обобщая решение предметной задачи, учитель ставит перед классом учебную задачу: «Сформулируйте алгоритм (правило) нахождения расстояния между двумя точками на местности с использованием карты».
После повторного обсуждения шагов исходной задачи итоговый алгоритм представляется в следующем виде:
1) определяем масштаб карты;
2) измеряем длину отрезка на карте между двумя пунктами;
3) обозначаем длину отрезка на местности (в сантиметрах) буквой x и находим отношение длины отрезка на карте к длине отрезка на местности, которое и будет равно масштабу карты;
4) решаем полученное уравнение и находим искомое расстояние.
Большим потенциалом для организации исследовательской работы учащихся с постановкой проблемных учебных задач с целью выявления и формулирования ключевых алгоритмов обладает стереометрический курс (X – XI классы).
Рассмотрим один из вариантов обсуждения на уроках геометрии по теме «Решение геометрических задач с помощью координат», одной из целей которого является вывод учащимися алгоритмов решения задач методом координат.
Первоначально учитель акцентирует внимание учащихся на том, что с помощью координат (методом координат) решаются задачи двух типов:
1-й тип – задачи на нахождение зависимости между элементами данной фигуры;
2-й тип – задачи на составление уравнения данной фигуры, если известны характеристические свойства точек этой фигуры (нахождение уравнения геометрического места точек). Преимущество метода координат состоит в том, что он позволяет кратко записывать формулировки задач или теорем и их решения.
В качестве примера рассмотрим предметную задачу на применение признака перпендикулярности прямой и плоскости и решим ее двумя способами. Учитель предлагает ребятам самостоятельно определить тип рассматриваемой задачи (задача относится к I типу).
Задача. Доказать, что плоскость, проходящая через концы трех ребер куба, исходящих из одной вершины, перпендикулярна диагонали куба, исходящей из той же вершины.
При решении задачи первым способом происходит обсуждение о приведенных в условии задачи геометрических объектах (прямая, плоскость) и их зависимости (отношение перпендикулярности). Возникает необходимость в актуализации признака перпендикулярности прямой и плоскости (если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости). Значит, следует выявить, какая пара пересекающихся прямых, лежащих в плоскости, определяемой концами трех ребер куба, исходящих из одной вершины, перпендикулярна диагонали куба, исходящей из той же вершины. Таким образом, перешли к обсуждению перпендикулярности прямых в пространстве, откуда возникает необходимость в напоминании определения перпендикулярных прямых в пространстве (две прямые в пространстве перпендикулярны, если угол между ними равен ), а также доказательству их перпендикулярности.
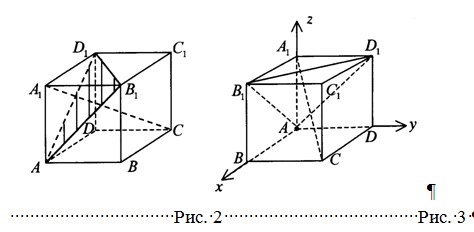
Опишем ход доказательства. По признаку перпендикулярности прямой и плоскости прямая будет перпендикулярна плоскости (рис. 2), если .
Докажем, что . Прямая перпендикулярна плоскости , так как (как диагонали в грани куба) и (исходя из того, что прямая перпендикулярна плоскости верхнего основания куба , а прямая лежит в этой плоскости). Итак, , значит, , поскольку прямая лежит в плоскости .
Аналогично доказывается, что .
Имеем: и . По признаку перпендикулярности прямой и плоскости , что и требовалось доказать.
Поскольку с координатами учащиеся хорошо знакомы, исходя из планиметрического курса геометрии, то рекомендуется доказательство задачи провести одновременно с обсуждением шагов и выявления алгоритма решения координатным методом.
Перед учащимися ставится учебная задача в виде вопроса: «Как решить задачу методом координат?».
1-й шаг. Осуществляем оптимальный ввод системы координат: выбираем начало координат и направления осей. Обычно в качестве осей координат выбираются прямые, фигурирующие в условии задачи, а также оси симметрии (если таковые имеются) тел, рассматриваемых в задаче. Желательно, чтобы система координат естественным образом определялась условием задачи.
В нашем случае введем систему координат с началом в точке А и направлениями осей вдоль ребер АВ, АD, соответственно. (Рис. 3)
2-й шаг. Условие задачи переводим с геометрического языка на координатный.
Поскольку в задаче фигурируют прямая и плоскость , то достаточно определить координаты точек (вершин куба) А, С, , , . Пусть длина ребра куба равна а. Имеем: А(0; 0; 0), С(а; а; 0), (0; 0; а), (а; 0; а), (0; а; а).
Поскольку, как и в первом способе решения задачи, необходимо доказать, что и , значит, нужно задать координаты векторам , и . Имеем: (а; а; - а), (а; - а; 0), (а; 0; а).
3-й шаг. Решение задачи проводим с помощью алгебраических вычислений.
Скалярно перемножим векторы и , а также и :
, .
Скалярное произведение данных векторов равно нулю, значит, угол между векторами равен .
4-й шаг. Заключение решения задачи интерпретируем в геометрическом виде.
Имеем: и , отсюда следует: (по признаку перпендикулярности прямой и плоскости), что и требовалось доказать.
Далее предлагается ученикам сравнить два способа решения задачи и выбрать из них рациональный. Несомненно, что второй способ более лаконичный, поскольку не требует введения вспомогательных элементов (плоскостей , ) при решении задачи.
Ярким примером для создания проблемной ситуации на уроках геометрии с целью поиска алгоритма решения геометрических задач II типа, задач на нахождение уравнения геометрического места точек, является следующее предметное задание: «Найти геометрическое место точек пространства, расстояние от которых до данной точки А(a; b; c) меньше либо равно R. Чем является данное геометрическое место точек?».
Ход обсуждения решения задачи рекомендуется провести пошагово, вследствие чего и выявится искомый алгоритм.
1-й шаг. Рассмотрим произвольную точку М из множества данного геометрического места точек и зададим ей координаты: М(x; y; z).
2-й шаг. В буквенных выражениях распишем общее свойство геометрического места точек. В нашем случае акцентируется внимание на расстоянии между двумя точками в пространстве А и М, которое меньше либо равно R. Имеем: .
3-й шаг. Выразим через координаты полученное свойство и выполним алгебраические преобразования:
Получили уравнение шара.
Таким образом, изучение математики с использованием учебных задач на открытие алгоритмов и правил способствует достижению эффективности процесса обучения, так как речь идет не просто о передаче системы знаний, формировании универсальных учебных действий, а о развитии учащегося, о его активном включении в образовательный процесс, что соответствует современным целям обучения в школе.
Использование проблемного обучения на уроках математики помогает вызвать определенную познавательную потребность у учащихся и создать внутренние условия для успешного последующего усвоения материала. Технология проблемного обучения позволяет с помощью проблемных вопросов и учебных задач включить учащихся в исследовательскую деятельность, в том числе с целью открытия и построения алгоритмов, структурно-логических схем для решения предметных задач.
Приведем фрагмент урока математики в VI классе по теме «Масштаб» с использованием учебной задачи, направленной на самостоятельное открытие учениками алгоритма нахождения расстояния между двумя точками.
Вначале учащимся предлагается решить предметную задачу: «Определите время в пути автобуса, следующего из г. Казани в г. Елабугу, если скорость автобуса равна 60 км/ч.». При решении задания учащиеся сталкиваются с необходимостью узнать расстояние от одного города до другого, что определяется с помощью карты Татарстана. (Рис. 1)

Рис. 1. Карта Татарстана.
В ходе беседы формулируется проблемный вопрос: как определить отношение длины отрезка на карте к длине соответствующего отрезка на местности?
В рассмотренном нами примере масштаб карты равен 1:30000000. Измерим длину отрезка на карте между двумя городами. Длина отрезка равна 6,1 см.
Обозначим длину отрезка на местности (в сантиметрах) буквой x и найдем отношение длины отрезка на карте к длине отрезка на местности: 6,1 : x, которое и будет равно масштабу карты. Значит, 6,1 : x = 1 : 30000000.
Решив полученное уравнение, имеем: x = = 183000000 (см) = 183000 (м) = 183 (км).
Возвращаясь к исходной задаче, определяем время в пути автобуса: t = ; t = = = 3,05 (ч).
Обобщая решение предметной задачи, учитель ставит перед классом учебную задачу: «Сформулируйте алгоритм (правило) нахождения расстояния между двумя точками на местности с использованием карты».
После повторного обсуждения шагов исходной задачи итоговый алгоритм представляется в следующем виде:
1) определяем масштаб карты;
2) измеряем длину отрезка на карте между двумя пунктами;
3) обозначаем длину отрезка на местности (в сантиметрах) буквой x и находим отношение длины отрезка на карте к длине отрезка на местности, которое и будет равно масштабу карты;
4) решаем полученное уравнение и находим искомое расстояние.
Большим потенциалом для организации исследовательской работы учащихся с постановкой проблемных учебных задач с целью выявления и формулирования ключевых алгоритмов обладает стереометрический курс (X – XI классы).
Рассмотрим один из вариантов обсуждения на уроках геометрии по теме «Решение геометрических задач с помощью координат», одной из целей которого является вывод учащимися алгоритмов решения задач методом координат.
Первоначально учитель акцентирует внимание учащихся на том, что с помощью координат (методом координат) решаются задачи двух типов:
1-й тип – задачи на нахождение зависимости между элементами данной фигуры;
2-й тип – задачи на составление уравнения данной фигуры, если известны характеристические свойства точек этой фигуры (нахождение уравнения геометрического места точек). Преимущество метода координат состоит в том, что он позволяет кратко записывать формулировки задач или теорем и их решения.
В качестве примера рассмотрим предметную задачу на применение признака перпендикулярности прямой и плоскости и решим ее двумя способами. Учитель предлагает ребятам самостоятельно определить тип рассматриваемой задачи (задача относится к I типу).
Задача. Доказать, что плоскость, проходящая через концы трех ребер куба, исходящих из одной вершины, перпендикулярна диагонали куба, исходящей из той же вершины.
При решении задачи первым способом происходит обсуждение о приведенных в условии задачи геометрических объектах (прямая, плоскость) и их зависимости (отношение перпендикулярности). Возникает необходимость в актуализации признака перпендикулярности прямой и плоскости (если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости). Значит, следует выявить, какая пара пересекающихся прямых, лежащих в плоскости, определяемой концами трех ребер куба, исходящих из одной вершины, перпендикулярна диагонали куба, исходящей из той же вершины. Таким образом, перешли к обсуждению перпендикулярности прямых в пространстве, откуда возникает необходимость в напоминании определения перпендикулярных прямых в пространстве (две прямые в пространстве перпендикулярны, если угол между ними равен ), а также доказательству их перпендикулярности.
Опишем ход доказательства. По признаку перпендикулярности прямой и плоскости прямая будет перпендикулярна плоскости (рис. 2), если .
Докажем, что . Прямая перпендикулярна плоскости , так как (как диагонали в грани куба) и (исходя из того, что прямая перпендикулярна плоскости верхнего основания куба , а прямая лежит в этой плоскости). Итак, , значит, , поскольку прямая лежит в плоскости .
Аналогично доказывается, что .
Имеем: и . По признаку перпендикулярности прямой и плоскости , что и требовалось доказать.

Заметим, что приведенный способ доказательства достаточно трудоемкий, требующий четкого представления учениками логического процесса взаимосвязи сужденийМетод координат, в свою очередь, позволяет упростить решение задачи.
Поскольку с координатами учащиеся хорошо знакомы, исходя из планиметрического курса геометрии, то рекомендуется доказательство задачи провести одновременно с обсуждением шагов и выявления алгоритма решения координатным методом.
Перед учащимися ставится учебная задача в виде вопроса: «Как решить задачу методом координат?».
1-й шаг. Осуществляем оптимальный ввод системы координат: выбираем начало координат и направления осей. Обычно в качестве осей координат выбираются прямые, фигурирующие в условии задачи, а также оси симметрии (если таковые имеются) тел, рассматриваемых в задаче. Желательно, чтобы система координат естественным образом определялась условием задачи.
В нашем случае введем систему координат с началом в точке А и направлениями осей вдоль ребер АВ, АD, соответственно. (Рис. 3)
2-й шаг. Условие задачи переводим с геометрического языка на координатный.
Поскольку в задаче фигурируют прямая и плоскость , то достаточно определить координаты точек (вершин куба) А, С, , , . Пусть длина ребра куба равна а. Имеем: А(0; 0; 0), С(а; а; 0), (0; 0; а), (а; 0; а), (0; а; а).
Поскольку, как и в первом способе решения задачи, необходимо доказать, что и , значит, нужно задать координаты векторам , и . Имеем: (а; а; - а), (а; - а; 0), (а; 0; а).
3-й шаг. Решение задачи проводим с помощью алгебраических вычислений.
Скалярно перемножим векторы и , а также и :
, .
Скалярное произведение данных векторов равно нулю, значит, угол между векторами равен .
4-й шаг. Заключение решения задачи интерпретируем в геометрическом виде.
Имеем: и , отсюда следует: (по признаку перпендикулярности прямой и плоскости), что и требовалось доказать.
Далее предлагается ученикам сравнить два способа решения задачи и выбрать из них рациональный. Несомненно, что второй способ более лаконичный, поскольку не требует введения вспомогательных элементов (плоскостей , ) при решении задачи.
Ярким примером для создания проблемной ситуации на уроках геометрии с целью поиска алгоритма решения геометрических задач II типа, задач на нахождение уравнения геометрического места точек, является следующее предметное задание: «Найти геометрическое место точек пространства, расстояние от которых до данной точки А(a; b; c) меньше либо равно R. Чем является данное геометрическое место точек?».
Ход обсуждения решения задачи рекомендуется провести пошагово, вследствие чего и выявится искомый алгоритм.
1-й шаг. Рассмотрим произвольную точку М из множества данного геометрического места точек и зададим ей координаты: М(x; y; z).
2-й шаг. В буквенных выражениях распишем общее свойство геометрического места точек. В нашем случае акцентируется внимание на расстоянии между двумя точками в пространстве А и М, которое меньше либо равно R. Имеем: .
3-й шаг. Выразим через координаты полученное свойство и выполним алгебраические преобразования:
Получили уравнение шара.
Таким образом, изучение математики с использованием учебных задач на открытие алгоритмов и правил способствует достижению эффективности процесса обучения, так как речь идет не просто о передаче системы знаний, формировании универсальных учебных действий, а о развитии учащегося, о его активном включении в образовательный процесс, что соответствует современным целям обучения в школе.












Комментарийлар